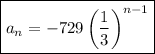Question

NO LINKS!!! URGENT HELP PLEASE!!!

Write a rule for the nth of the geometric sequence.

17. a_3 = 8, a_6 = 64

18. a_4 = -27, a_6 = -3

Answer 1

`\textsf{17.} \quad a_n=2(2)^(n-1)`

`\textsf{18.} \quad a_n=-729 \left((1)/(3)\right)^(n-1)`

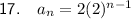
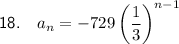
Explanation:

To write a rule for the nth term of a geometric sequence, we can use the following formula:

`\boxed{\begin{minipage}{5.5 cm}\underline{Geometric sequence}\\\\$a_n=ar^(n-1)$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the first term. \\\phantom{ww}$\bullet$ $r$ is the common ratio.\\\phantom{ww}$\bullet$ $a_n$ is the $n$th term.\\\phantom{ww}$\bullet$ $n$ is the position of the term.\\\end{minipage}}`

`\hrulefill`

Question 17

Given terms:

• a₃ = 8
• a₆ = 64

Substitute the given values into the formula to create two equations:

`\begin{aligned}a_3=ar^(3-1)&=8\\ar^2&=8\end{aligned}`

`\begin{aligned}a_6=ar^(6-1)&=64\\ar^5&=64\end{aligned}`

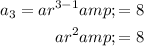
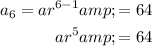
To find the common ratio, r, divide the second equation by the first equation to eliminate a:

`(ar^5)/(ar^2)=(64)/(8)`

`(r^5)/(r^2)=8`

`r^(5-2)=8`

`r^3=8`

`r^3=2^3`

`r=2`

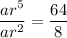
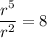
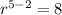
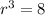
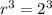
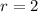
Substitute the found value of r into one of the equations and solve for a:

`\begin{aligned}a(2)^2&=8\\4a&=8\\(4a)/(4)&=(8)/(4)\\a&=2\end{aligned}`

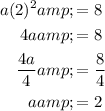
Therefore, the rule for the nth term of the given geometric sequence is:

`\boxed{a_n=2(2)^(n-1)}`

`\hrulefill`

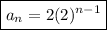
Question 18

Given terms:

• a₄ = -27
• a₆ = -3

Substitute the given values into the formula to create two equations:

`\begin{aligned}a_4=ar^(4-1)&=-27\\ar^3&=-27\end{aligned}`

`\begin{aligned}a_6=ar^(6-1)&=-3\\ar^5&=-3\end{aligned}`

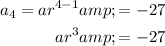
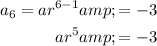
To find the common ratio, r, divide the second equation by the first equation to eliminate a:

`(ar^5)/(ar^3)=(-3)/(-27)`

`(r^5)/(r^3)=(1)/(9)`

`r^(5-3)=(1)/(9)`

`r^(2)=(1)/(9)`

`r=\sqrt{(1)/(9)}`

`r=(1)/(3)`

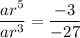
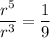
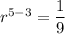
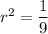
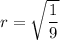
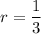
Substitute the found value of r into one of the equations and solve for a:

`\begin{aligned}a\left((1)/(3)\right)^3&=-27\\(1)/(27)a&=-27\\a&=-729\end{aligned}`

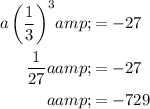
Therefore, the rule for the nth term of the given geometric sequence is:

`\boxed{a_n=-729 \left((1)/(3)\right)^(n-1)}`