Question

What is required for two triangles to be similar?

Answer 1

Definition VS Theorem

Definition: In order for two triangles to be classified as "similar" triangles, each triangle's angles must be congruent with the corresponding angle of the other triangle, and each of their three corresponding side pairs must all form a common ratio.

Theorems: Proving just some of those 6 parts is sufficient to prove triangle Similarity, specifically: SSS, SAS, or AA

Explanation:

In order for two triangles to be classified as "similar" triangles, their corresponding angles must be congruent, and their corresponding side pairs must all form a common ratio.

This means that to prove
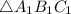`\triangle A_1B_1C_1` is similar to
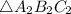`\triangle A_2B_2C_2`, we'd need to prove

`\angle A_1 \cong \angle A_2`,

`\angle B_1 \cong \angle B_2`, and

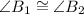`\angle C_1 \cong \angle C_2`,

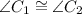as well as prove that there exists a single positive number "k" such that the following equation is true for the ratios of corresponding side lengths:

`(A_1B_1)/(A_2B_2)=(B_1C_1)/(B_2C_2)=(A_1C_1)/(A_2C_2)=k`

Fortunately, instead of finding all of those quantities, and proving all 6 of those things true, there are several theorems that allow us to prove less than all 6 of those things, yet still be sufficient to prove that the triangles are similar.

Note that if two Triangles are Congruent, then they are Similar. It is a special case of Similar Triangles where k=1.

To deal with all of the triangles that are Similar but not Congruent, there are three cases where triangle must be Similar:

SSS (Side-Side-Side)

SAS (Side-Angle-Side)

AA (Angle-Angle)

WARNING: Even though SSS looks just like SSS for Triangle congruence, Similarity, is different than congruence. We're doing a different thing for similarity. For these three Similarity rules, angles must be proven congruent, and corresponding sides must form a ratio that is common to all of the other corresponding side ratios for the theorem.

SSS (Side-Side-Side)

If all three corresponding side pairs form a common ratio, that's enough. It will force the corresponding angles to be congruent.

SAS (Side-Angle-Side)

Here, if two corresponding side pairs form a common ratio, AND if the corresponding angles between those two sides on each triangle are congruent, then the two triangles must be Similar.

AA (Angle-Angle)

Here, if just any two corresponding angle pairs are congruent, then the two triangles must be Similar. This is enough to force the third angle pair to be congruent, and all of the corresponding side pairs to have a common ratio.

Answer 2

SSS, SAS, AAS, or ASA.

Explanation:

SSS refers to all three sides being congruent with the two triangles you're comparing.

SAS refers to one angle between two congruent sides with the two triangles you're comparing.

AAS refers to one angle and one side between an angle with the two triangles you're comparing.

ASA refers to two congruent angles between a side with the two triangles you're comparing.