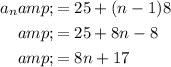Question

NO LINKS!!! URGENT HELP PLEASE!!!!!

Write a rule for the nth term of the arithmetic sequence that has the two given terms.

7. a_2 = 17, a_11 = 35

8. a_9 = 89, a_15 = 137

Answer 1

`\textsf{7.} \quad a_n=2n+13`

`\textsf{8.} \quad a_n=8n+17`

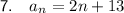
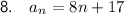
Explanation:

To write a rule for the nth term of a arithmetic sequence, we can use the following formula:

`\boxed{\begin{minipage}{8 cm}\underline{General form of an arithmetic sequence}\\\\$a_n=a+(n-1)d$\\\\where:\\\phantom{ww}$\bullet$ $a_n$ is the nth term. \\ \phantom{ww}$\bullet$ $a$ is the first term.\\\phantom{ww}$\bullet$ $d$ is the common difference between terms.\\\phantom{ww}$\bullet$ $n$ is the position of the term.\\\end{minipage}}`

`\hrulefill`

Question 7

Given terms:

• a₂ = 17
• a₁₁ = 35

Substitute the given values into the formula to create two equations:

`\begin{aligned}a_2=a+(2-1)d&=17\\a+d&=17\end{aligned}`

`\begin{aligned}a_(11)=a+(11-1)d&=35\\a+10d&=35\end{aligned}`

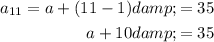
Rearrange the first equation to isolate d:

`d=17-a`

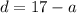
Substitute this into the second equation and solve for a:

`\begin{aligned}a+10(17-a)&=35\\a+170-10a&=35\\170-9a&=35\\-9a&=-135\\a&=15\end{aligned}`

Substitute the found value of a into the equation for d and solve for d:

`d=17-15=2`

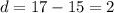
Therefore, the rule for the nth term of the given arithmetic sequence is:

`\begin{aligned}a_n&=15+(n-1)2\\ &=15+2n-2\\&=2n+13\end{aligned}`

`\hrulefill`

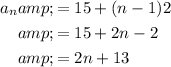
Question 8

Given terms:

• a₉ = 89
• a₁₅ = 137

Substitute the given values into the formula to create two equations:

`\begin{aligned}a_9=a+(9-1)d&=89\\a+8d&=89\end{aligned}`

`\begin{aligned}a_(15)=a+(15-1)d&=137\\a+14d&=137\end{aligned}`

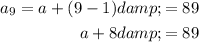
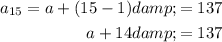
Rearrange the first equation to isolate a:

`a=89-8d`

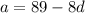
Substitute this into the second equation and solve for d:

`\begin{aligned}a+14d&=137\\(89-8d)+14d&=137\\89+6d&=137\\6d&=48\\d&=8\end{aligned}`

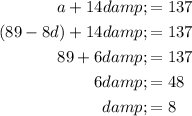
Substitute the found value of d into the equation for a and solve for a:

`\begin{aligned}a&=89-8(8)\\&=89-64\\&=25\end{aligned}`

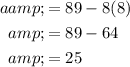
Therefore, the rule for the nth term of the given arithmetic sequence is:

`\begin{aligned}a_n&=25+(n-1)8\\ &=25+8n-8\\&=8n+17\end{aligned}`