Answer:
 or
or
 or
or
 or
or

Explanation:
You can use a substitution and treat it as a quadratic equation.
Let u = x^2.
y = -8x^4 + 3x² + 9
Apply the substitution.
y = -8u² + 3u + 9
-8u² + 3u + 9 = 0
8u² - 3u - 9 = 0
Use the quadratic formula to solve for u.
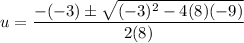
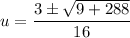
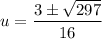
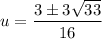
 or
or
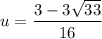
Remember that u = x², so now we substitute back x² for u.
 or
or
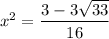
 or
or
 or
or
 or
or

Two of those roots are complex, so we deal with that now.
 or
or
 or
or
 or
or
