Question

Two points, A and C, are marked on the

coordinate grid below.
A and C are diagonally opposite vertices of
a square.
Work out the coordinates of the other two
vertices of the square.

Answer 1

Answer: (5,6) and (8,3)

Explanation:

Answer 2

The coordinates of B and D are given by:

B(4.5−
`3√(2) /2`,6.5−
`3√(2) /2`)

D(4.5−
`3√(2) /2` ,6.5−
`3√(2) /2`)

Calculate the Midpoint (M) between A and C:

The midpoint is found by averaging the x-coordinates and y-coordinates.

M( x1+x2/2, y1+y2/2)

M( 3+6/2, 5+8/2)

M(4.5,6.5)

Calculate the Distance from A to C:

Use the distance formula to find the distance between A and C

Distance=
`√(x2 - x1)^2 + √(y2 - y1)^2`

Distance=
`(6−3)^2 + (8−5)^2`

Distance=
`3^2 + 3^2`

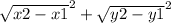
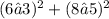
Distance = 18

Distance =
`3√(2)`

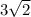
​Calculate the Coordinates of B and D:

The coordinates of B and D are found by moving from the midpoint (M) a distance equal to half the distance from A to C.

B(4.5+
`3√(2) /2`,6.5+
`3√(2) /2`)

B(4.5−
`3√(2) /2`,6.5−
`3√(2) /2`)

B(4.5−
`3√(2) /2`,6.5−
`3√(2) /2`)

D(4.5−
`3√(2) /2` ,6.5−
`3√(2) /2` )

So, the coordinates of B and D are given by:

B(4.5−
`3√(2) /2`,6.5−
`3√(2) /2`)

D(4.5−
`3√(2) /2` ,6.5−
`3√(2) /2`)

These are the coordinates of the other two vertices of the square.