Answer:
2 and 8
Explanation:
Using the given information, we can represent the numbers (a and b) in a system of equations:
eq 1. "the sum of two numbers is 10"
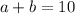
eq 2. "the sum of their square is 68"

Then, we can solve for each number using substitution.
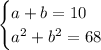
We can first solve for a in terms of b in the first equation.
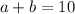
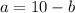
Then, we can substitute this a-value into the second equation and solve for b.

↓ substituting the solution for a in terms of b
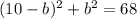
↓ expanding the binomial ...
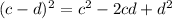

↓ simplifying
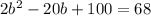
↓ subtracting 68 from both sides
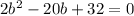
↓ dividing both sides by 2
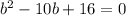
↓ factoring ...
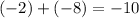 and
and
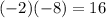

↓ solving for b ... if
 , then
, then
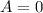 or
or
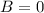
b = 2 or b = 8
Now, we can try plugging each b-value into the solution for a in terms of b, then solve for a.
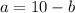
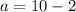

OR
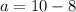
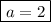
So, the two numbers are 2 and 8.