Question

Please help me and win 100 points for helping out NO NONSENSE AWNSERS PLEASE.

what are the first four terms of a geometric sequence if its a common ratio is 8 and its first term is 1.6

A. 1.6,-6.4,-14.4,-22.4
B. 1.6,12.8,102.4,819.2
C.1,6,9.6,17.6,25.6
D.1.6,0.2,0.025,0.003125

Answer 1

B. 1.6, 12.8, 102.4, 819.2

Explanation:

The formula for the nth term of a geometric sequence is:

`\boxed{a_n=ar^(n-1)}`

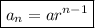
where:

• a is the first term.
• r is the common ratio.

If the first term is 1.6, then a = 1.6.

If the common ratio is 8, then r = 8.

Substitute the given values of a and r into the formula to create an equation for the nth term:

`a_n=1.6 \cdot 8^(n-1)`

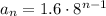
To find the first four terms of the sequence, substitute the n-values 1 through 4 into the nth term equation:

`\begin{aligned}a_1&=1.6\cdot 8^(1-1)\\&=1.6\cdot 8^(0)\\&=1.6\cdot 1\\&=1.6\end{aligned}`
`\begin{aligned}a_2&=1.6\cdot 8^(2-1)\\&=1.6\cdot 8^(1)\\&=1.6\cdot 8\\&=12.8\end{aligned}`

`\begin{aligned}a_3&=1.6\cdot 8^(3-1)\\&=1.6\cdot 8^(2)\\&=1.6\cdot 64\\&=102.4\end{aligned}`
`\begin{aligned}a_4&=1.6\cdot 8^(4-1)\\&=1.6\cdot 8^(3)\\&=1.6\cdot 512\\&=819.2\end{aligned}`

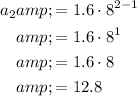
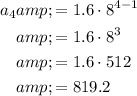
Therefore, the first four terms of the geometric sequence are:

• 1.6, 12.8, 102.4, 819.2