Answer:
q = 8.57 10⁻⁵ mC
Step-by-step explanation:
For this exercise let's use Newton's second law
F = ma
where force is magnetic force
F = q v x B
the bold are vectors, if we write the module of this expression we have
F = qv B sin θ
as the particle moves perpendicular to the field, the angle is θ= 90º
F = q vB
the acceleration of the particle is centripetal
a = v² / r
we substitute
qvB = m v² / r
qBr = m v
q =
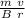
The exercise indicates the time it takes in the route that is carried out with constant speed, therefore we can use
v = d / t
the distance is ¼ of the circle,
d =
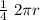
d =
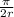
we substitute
v =
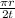
r =
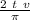
let's calculate
r =
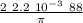 2 2.2 10-3 88 /πpi
2 2.2 10-3 88 /πpi
r = 123.25 m
let's substitute the values
q =
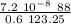 7.2 10-8 88 / 0.6 123.25
7.2 10-8 88 / 0.6 123.25
q = 8.57 10⁻⁸ C
Let's reduce to mC
q = 8.57 10⁻⁸ C (10³ mC / 1C)
q = 8.57 10⁻⁵ mC