Question

A 25g bullet is fired into a 2.0 kg block of wood initially at rest. The block and imbedded bullet then start moving at 4.0 m/s. Using the conservation of momentum, find the initial velocity of the bullet.

Answer 1

`\vec v_{0_(b)}=324 \ m/s`

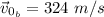
Conceptual:

Using the idea of momentum conservation to answer this question.

What is momentum?

Momentum is a quantity an object has as it is in motion and is the product of that objects mass and velocity. Momentum is a conservable quantity as long as there are no external forces acting on the system. Momentum is measured in (kg·m²)/s and it is a vector quantity. We can calculate momentum using the following formula.

`\boxed{\left\begin{array}{ccc}\text{\underline{Formula for Momentum:}}\\\\ \vec P=m \vec v\end{array}\right}`

Step-by-step:

Given:

`m_b=25 \ g \rightarrow 0.025 \ kg\\m_w= 2.0\ kg\\\vec v_{f_(bw)}=4.0 \ m/s`

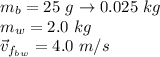
Find:

`\vec v_{o_(b)}= \ ?? \ m/s`

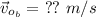
In order to tackle this problem we need to analyze the objects before the collision and after the collision.

The initial momentum of the system:

`\underline{ \vec P_0}\\\\\vec P_{0_(b)}=m_b \vec v_{0_(b)} \rightarrow (0.025)\vec v_{0_(b)}\\\\\vec P_{0_(w)}=m_w \vec v_{0_(w)} \rightarrow (2)(0)\\+ \rule{100}{0.5pt}\\\boxed{\vec P_0= (0.025)\vec v_{0_(b)}}`

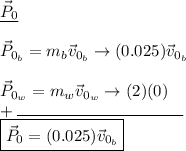
The final momentum of the system:

At this point the bullet is embedded in the wood so we can treat them as one object.

`\underline{\vec P_f}\\\\\vec P_{f_(bw)}=(m_b+m_w) \vec v_{f_(bw)} \rightarrow (.025+2)(4) =8.1\\\\\therefore\boxed{\vec P_(f)=8.1}`

Momentum is conserved. Thus, the initial momentum of the system must equal the final momentum of the system.

`\vec P_(0)=\vec P_(f)\\\\\Longrightarrow 0.025 \vec v_{0_(b)}=8.1\\\\\Longrightarrow \vec v_{0_(b)}=(8.1)/(.025)\\ \\\therefore \boxed{\boxed{\vec v_{0_(b)}=324 \ m/s}}`

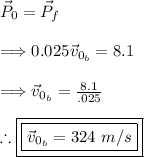
Thus, the bullet's initial velocity was found.