Question

What concentration of acid is needed to completely neutralize 25.0 mL of 1.5 M NaOH, if it takes exactly 12.5 mL to

reach the endpoint of the titration? (show your work!)

Answer 1

The concentration of acid which is needed to completely neutralize 25.0 mL of 1.5 M NaOH, if it takes exactly 12.5 mL to reach the endpoint of the titration would be 3M.

We know that at the equivalence point in a neutralization, the moles of acid are equal to the moles of base.

`\qquad\longrightarrow \sf Moles_((Acid)) = Moles_((Base))\\`

`\footnotesize{ \longrightarrow \sf Volume_((Acid))* Concentration_((Acid)) = Volume_((Base))* Concentration_((Base))} \\`

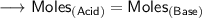
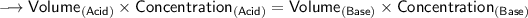
According to the specific parameters-

• 
  `\sf Volume_((Acid)) = 12.5 mL\\`

• 
  `\sf Volume_((Base))= 25 mL\\`

• 
  `\sf Concentration_((Base)) = 1.5 M \\`

Now that we have all the required values,so we can plug them into the formula and solve for concentration of acid -

`\footnotesize{\longrightarrow \sf Volume_((Acid))* Concentration_((Acid)) = Volume_((NaOH))* Concentration_((NaOH)) }\\`

`\longrightarrow \sf 12.5 \: mL * Concentration_((Acid)) = 25 \:mL * 1.5\: M \\`

`\longrightarrow \sf Concentration_((Acid)) = (25 \:mL * 1.5\: M )/(12.5\:mL)\\`

`\longrightarrow \sf Concentration_((Acid)) = \frac{37.5\:\cancel{mL} \: M }{12.5\:\cancel{mL}}\\`

`\longrightarrow \sf Concentration_((Acid)) = (37.5\:M)/(12.5)\\`

`\longrightarrow \sf Concentration_((Acid)) = \frac{\cancel{37.5}\:M}{\cancel{12.5}}\\`

`\qquad\longrightarrow \sf \underline{Concentration_((Acid)) = \boxed{\sf{3\:M }}}\\`

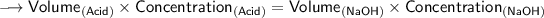
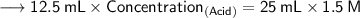
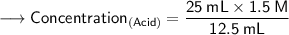
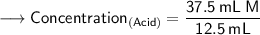
• Henceforth, the concentration would be 3M.