Question

Paddy and Anna each invest $2000 for 5 years.

Paddy earns simple interest at a rate of 1.25% per year.

Anna earns compound interest at a rate of r% per year.

At the end of 5 years, Paddy's investment is worth the same as Anna's investment.

Calculate the value of r.

Answer 1

Answer: r= 1.22

Explanation:

Formula for amount with simple interest =
`P(1+rt)`

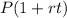
, where

P= principal value , r= rate of interest , t = time.

Given: P= $2000, t= 5 years, r= 1.25% = 0.0125

`A=2000(1+0.0125*5)\\\\=2000(1.0625)=2125`

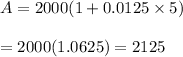
Formula to compute compound amount :
`P(1+r)^t`

`=2000(1+r)^5`

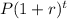
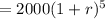
When both have same worth then

`2000(1+r)^5=2125\\\\\\ (1+r)^5=(2125)/(2000)\\\\\\ (1+r)^5=1.0625`

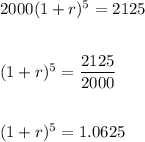
taking log on both sides , we get

`5\ln (1+r)=\ln 1.0625\\\\\\ 5\ln (1+r)=0.0606246\\\\\\ \ln (1+r)=0.012125\\\\\\ 1+r=e^(0.005266)\\\\\\ 1+r=1.0122\\\\ r=0.0122\\\\ \\ r=1.22\%`

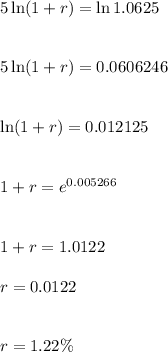
Hence, Value of r= 1.22