Question

a ball is thrown directly downward with an initial speed of 8.45 m/s, from a height of 29.8m. After what time interval does it strike the ground?

Answer 1

Approximately
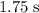`1.75\; {\rm s}` (assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}` and that air resistance is negligible.)

Step-by-step explanation:

Find the velocity of the ball right before landing using the following SUVAT equation:

`\displaystyle v^(2) - u^(2) = 2\, a\, x`,

Where:

• 
  `v` is the velocity of the ball right before landing,
• 
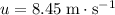  `u = 8.45\; {\rm m\cdot s^(-1)}` is the initial velocity,
• 
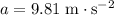  `a = 9.81\; {\rm m\cdot s^(-2)}` is the acceleration, and
• 
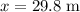  `x = 29.8\; {\rm m}` is the change in the height of the ball.

Rearrange this equation to find
`v`:

`\begin{aligned}v &= \sqrt{u^(2) + 2\, a\, x} \\ &= \sqrt{(8.45)^(2) + 2\, (9.81)\, (29.8)}\; {\rm m\cdot s^(-1)} \\ &\approx 25.61\; {\rm m\cdot s^(-1)}\end{aligned}`.

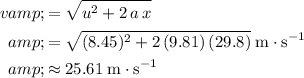Divide the change in velocity by acceleration to find the time elapsed:

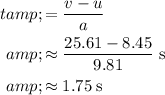`\begin{aligned}t &= (v - u)/(a) \\ &\approx (25.61 - 8.45)/(9.81) \; {\rm s}\\ &\approx 1.75\; {\rm s}\end{aligned}`.