Answer:
The probability that when a couple has five children, at least one of them is a girl is 31/32 or approximately
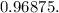
Step-by-step explanation:
We can determine the probability of having at least one girl by using the complement rule, which states that the probability of an event occurring is equal to one minus the probability of the event not occurring. In this case, the event of interest is having at least one girl among five children and the complement is having only boys among five children.
Since there are two equally likely outcomes (boy or girl) for each child and the events are independent, we can find the probability of having all boys by multiplying the probabilities of each individual event together: (1/2)^5 = 1/32.
So, the probability of having at least one girl is 1 - 1/32 = 31/32 or approximately 0.96875.