Question

A concrete foundation for a building has the shape of a rectangular prism. The foundation is 20 yards long, 13 yards wide, and 2 yards high. If concrete costs 5$ per cubic yard, how much did the concrete cost for the foundation?

Answer 1

The volume of the foundation can be calculated by multiplying its length, width, and height. Therefore, the volume is:

20 yards x 13 yards x 2 yards = 520 cubic yards

The cost of the concrete is $5 per cubic yard, so we can calculate the total cost by multiplying the volume by the cost per cubic yard. Therefore, the cost is:

520 cubic yards x $5 per cubic yard = $2,600

Therefore, the concrete for the foundation cost $2,600.

Answer 2

$2,600

Explanation:

To find the cost of the concrete foundation of a building in the shape of a rectangular prism, multiply its volume (in cubic yards) by the cost per cubic yard.

The volume of a rectangular prism is the product of its width, length and height.

`\boxed{V=w \cdot l \cdot h}`

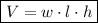
Given values:

• w = 13 yards
• l = 20 yards
• h = 2 yards

Therefore, the volume of the concrete foundation is:

`\begin{aligned}V&=13 \cdot 20 \cdot 2\\&=260 \cdot 2\\&=520\; \sf yd^3\end{aligned}`

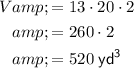
Given the concrete costs $5 per cubic yard, multiply the volume by the cost to calculate the total cost of the concrete for the foundation is:

`\begin{aligned}\textsf{Total cost}&=\sf Volume \cdot cost\\&=\sf 520 \; yd^3 \cdot \$5/yd^3\\&=\sf 520 \cdot \$5\\&= \sf \$2600\end{aligned}`

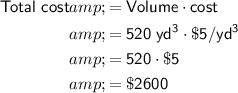
Therefore, the total cost of the concrete for the foundation is $2,600.