Question

7. If I || m. find the values of x and y in the diagram below. (7x-31) 63 | (5r-8) 63° (4y +27)* m 1 ​

Answer 1

x = 13, y = 24.

Explanation:

5x - 8 = 180 - (4y + 27) (Internal alternate angles are congruent)

Also 4y + 27 = 63 + (7x - 31) (External angle of a triangles theorem)

Simplifying the above 2 equations we get:

5x + 4y = 161 ........ (A)

7x - 4y = -5 ........ (B)

Adding A + B:

12x = 156

x = 13.

Now substitute x = 13 in equation A:

7(13) - 4y = -5

4y = 91 + 5 = 96

y = 24.

Answer 2

x = 13

y = 24

Explanation:

According to the Consecutive Interior Angles Theorem, when a straight line intersects two parallel straight lines, the resulting consecutive interior angles formed are supplementary (sum to 180°).

Therefore, as line l and line m are parallel, the angle marked (7x - 31)°, and the sum of the angles marked 63° and (5x - 8)°, are supplementary:

`(7x - 31)^(\circ)+63^(\circ)+(5x-8)^(\circ)=180^(\circ)`

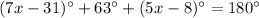
Solve the equation for x:

`7x - 31+63+5x-8=180`

`12x +24=180`

`12x +24-24=180-24`

`12x =156`

`(12x)/(12) =(156)/(12)`

`x=13`

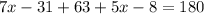
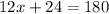
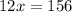
The exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles of the triangle. Therefore:

`(7x - 31)^(\circ)+63^(\circ)=(4y+27)^(\circ)`

Substitute the found value of x into the equation and solve for y:

`7x - 31+63=4y+27`

`7(13)- 31+63=4y+27`

`91- 31+63=4y+27`

`123=4y+27`

`123-27=4y+27-27`

`96=4y`

`4y=96`

`(4y)/(4)=(96)/(4)`

`y=24`

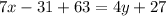
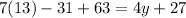
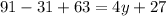
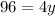
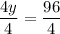
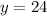
Therefore, the values of x and y are:

• x = 13
• y = 24