Answer:

Explanation:
Given
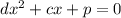
Let the roots be
 and
and
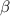
So:
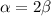
Required
Determine the relationship between d, c and p
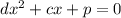
Divide through by d
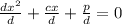

A quadratic equation has the form:

So:
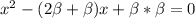
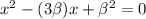
So, we have:
 -- (1)
-- (1)
and
 -- (2)
-- (2)
Make
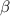 the subject in (1)
the subject in (1)

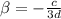
Substitute
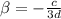 in (2)
in (2)

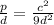
Multiply both sides by d
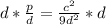
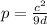
Cross Multiply
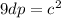
or

Hence, the relationship between d, c and p is:
