Question

2b

OAB is a triangle.
04.
OB -2b
Tis the point on AB such that AT: TB-5:1
Show that OT is parallel to the vector a + 2b
* Sa
Sa
B
T
Diagram NOT
accurately drawn

Answer 1

Answer: 85 degrees

Step-by-step so yk solve you need OA IS 5 and OB is 9 so then solve and you get the answer

Answer 2

`\overrightarrow{OT}=(5)/(6)(\text{a}+2\text{b})`

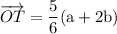
As vector OT is a scalar multiple of (a + 2b), then vector OT is parallel to (a + 2b).

Explanation:

Given vectors:

`\overrightarrow{OA}=5\text{a}`

`\overrightarrow{OB}=2\text{b}`

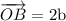
Find the vector AB using the given vectors:

`\begin{aligned}\overrightarrow{AB}&=\overrightarrow{AO}+\overrightarrow{OB}\\&=\overrightarrow{OB} - \overrightarrow{OA}\\&=2\text{b}-5\text{a}\end{aligned}`

If AT : TB = 5 : 1 then AT will be 5/6 of AB, and TB will be 1/6 of AB.

`\overrightarrow{AT}=(5)/(6)\overrightarrow{AB}=(5)/(6)(2\text{b}-5\text{a})`

`\overrightarrow{TB}=(1)/(6)\overrightarrow{AB}=(1)/(6)(2\text{b}-5\text{a})`

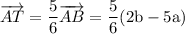
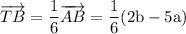
Now we have found vector AT, we can calculate vector OT:

`\begin{aligned}\overrightarrow{OT}&=\overrightarrow{OA}+\overrightarrow{AT}\\\\&=5\text{a}+(5)/(6)(2\text{b}-5\text{a})\\\\&=5\text{a}+(5)/(3)\text{b}-(25)/(6)\text{a}\\\\&=(5)/(6)\text{a}+(5)/(3)\text{b}\\\\&=(5)/(6)\text{a}+(10)/(6)\text{b}\\\\&=(5)/(6)(\text{a}+2\text{b})\\\\\end{aligned}`

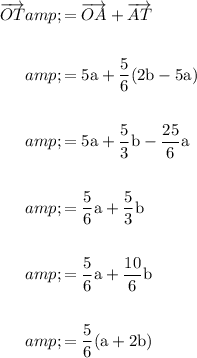
If two vectors are parallel, they are scalar multiples of each other.

Therefore, vectors that are parallel to (a + 2b) are in the form k(a + 2b), where k is the scalar multiple.

As vector OT is a scalar multiple of (a + 2b), where k = 5/6, this proves that vector OT is parallel to (a + 2b).