Question

True or False: The points (6,13) (21, 33) and (99, 137) all lie on the same line. The equation of the line is y = 4/3x + 5. PLS HELP ASAP

Answer 1

This is true look at picture for clarification

Answer 2

True

Explanation:

To see if the points all lie on the line y = 4/3x + 5, substitute their x and y values into the equation, solve, and see if the equation is true.

1) First, substitute the x and y values of (6,13) for the x and y in the equation and solve:

`13 = (4)/(3) (6) + 5 \\13 = (24)/(3) +(15)/(3) \\13 = (39)/(3)\\13 = 13`

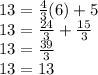
The result is a true equation. Thus, (6,13) is on the line.

2) Do the same with the point (21,33):

`33 = (4)/(3) (21) + 5 \\33 = (84)/(3) +(15)/(3) \\33 = (99)/(3) \\33 = 33`

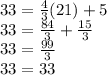
The result is a true equation. Thus, (21,33) is on the line.

3) Finally, do the same with (99, 137):

`137 = (4)/(3) (99) + 5\\137 = (396)/(3)+(15)/(3) \\137 = (411)/(3) \\137 = 137`

The result is a true equation. Thus, (99, 137).

All three points are on the line, thus the statement is true.