Question

A kite is flying 40 feet in the air. The kite string is 75 feet long and has been staked to the ground. To the

nearest degree, what is the measure of the angle made between the ground and the string of the kite?

Answer 1

32°

Explanation:

We can model the given scenario as a right triangle, where the height of the triangle is the vertical distance between the kite and the ground (40 feet), and the hypotenuse is the length of the kite's string (75 feet).

The angle made between the ground and string of the kite is the angle that is opposite the triangle's height.

As we have both the side of the triangle that is opposite the angle, and the hypotenuse of the triangle, we can use the sine trigonometric ratio to calculate the measure of the angle.

`\boxed{\begin{minipage}{9 cm}\underline{Sine trigonometric ratio} \\\\$\sf \sin(\theta)=(O)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

Given values:

• O = 40
• H = 75

Substitute the values into the sine ratio and solve for θ:

`\sin(\theta)=(40)/(75)`

`\theta=\sin^(-1)\left((40)/(75)\right)`

`\theta=32.2309526...^(\circ)`

`\theta=32^(\circ)\; \sf (nearest\;degree)`

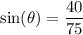
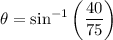
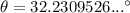
Therefore, the measure of the angle between the ground and the string of the kite is 32° (to the nearest degree).