Question

NO LINKS!! URGENT HELP PLEASE!!!!

Find the coordinates of point P along the directed line segment AB that partitions it so that the ratio of AP to PB is 2:1.

Answer 1

(2, 1)

Explanation:

If the line segment AB is partitioned so that the ratio of AP to PB is 2 : 1, then point P is two-thirds of the way along AB.

Point A is located at (-2, 3) and point B is located at point (4, 0).

Since the difference between the x and y values of points A and B are multiples of 3, we can visually partition AB into 3 sections of equal length by placing points at (0, 2) and (2, 1).

Therefore, as point P is two-thirds of the way along AB, point P is located at (2, 1).

To prove this mathematically, we can use the Section Formula for Internal Division:

`\boxed{\begin{minipage}{8.1 cm}\underline{Section Formula - Internal Division}\\\\\\$P(x,y)=\left((nx_1+mx_2)/(m+n),(ny_1+my_2)/(m+n)\right)$\\\\\\where:\\\phantom{ww} $\bullet$ $\overline{AB}$ is the directed line segment.\\\phantom{ww} $\bullet$ $A(x_1, y_1)$ and $B(x_2, y_2)$ are the endpoints.\\\phantom{ww} $\bullet$ Point $P$ divides the segment in the ratio $m : n$.\\ \end{minipage}}`

Given values:

• (x₁, y₁) = A = (-2, 3)
• (x₂, y₂) = B = (4, 0)
• m : n = 2 : 1

Substitute the values into the formula:

`\begin{aligned}P(x,y)&=\left((nx_1+mx_2)/(m+n),(ny_1+my_2)/(m+n)\right)\\\\&=\left((1 \cdot (-2)+2 \cdot 4)/(2+1),(1 \cdot 3+2 \cdot 0)/(2+1)\right)\\\\&=\left((-2+8)/(3),(3+0)/(3)\right)\\\\&=\left((6)/(3),(3)/(3)\right)\\\\&=\left(2,1\right)\end{aligned}`

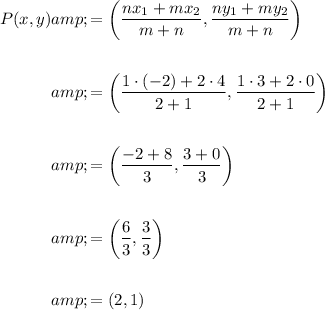
Hence proving the the location of point P on the coordinate plane is (2, 1).

Answer 2

coordinates of P are (2, 1).

Explanation:

Let P be the point that partitions the line segment AB such that AP: PB = 2:1.(m:n) Then we can use the line ratio formula:

`\bold{x = (xB * m + xA*n)/(m + n)}`

`\bold{y = (yB * m + yA*n)/(m + n)}`

where (xA, yA) and (xB, yB) are the coordinates of A and B respectively, and m is the ratio of AP to PB, which is 2:1.

Substituting the given values, we get:

`\bold{x = (4*2+ (-2)*1)/(2 + 1)}=2`

`\bold{y = (0 * 2 + 3*1)/(2 + 1)= 1}`

Therefore, the coordinates of P are (2, 1).