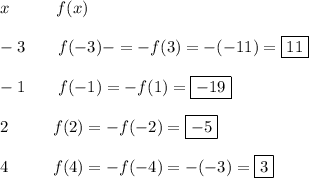Question

The table shows some values for an odd function f. Complete the table.

Answer 1

`\\x \quad\quad \;\;\;f(x)\\\\-3 \quad\quad f(-3) -= - f(3) = -(-11) = \boxed{11}\\\\-1\quad\quad f(-1) = -f(1) = \boxed{-19}\\\\2\quad\quad\:\:\: f(2) = - f(-2) = \boxed{- 5}\\\\4\quad\quad\:\:\:f(4) = - f(-4) = - (-3) = \boxed{3}`

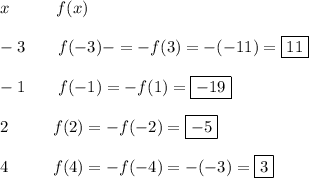
Explanation:

A function is "even" when:

`f(- x) = f(x) \textrm{\;for\;all\;x}`

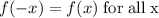
In other words there is symmetry about the y-axis (like a reflection):

A function is "odd" when

`f(-x) = -f(x) \textrm{ for all x}`
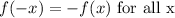
The symmetry is around the origin

Looking at the table and using the property of an odd function we can solve for the missing values

`\\x \quad\quad \;\;\;f(x)\\\\-3 \quad\quad f(-3) -= - f(3) = -(-11) = \boxed{11}\\\\-1\quad\quad f(-1) = -f(1) = \boxed{-19}\\\\2\quad\quad\:\:\: f(2) = - f(-2) = \boxed{- 5}\\\\4\quad\quad\:\:\:f(4) = - f(-4) = - (-3) = \boxed{3}`