In triangle PQR PQ equals 39 inches, PR equals 17 inches, and HTE altitude PN equals 15 inches. The correct answer is QR is, 44 in.
How did we figure this out?
Solution:
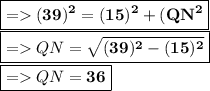
Now we have to determine the side RN.
Now put all the values in the above expression, we get the value of side RN.
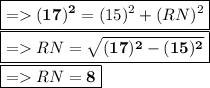
Therefore, In triangle PQR PQ equals 39 inches, PR equals 17 inches, and HTE altitude PN equals 15 inches. The correct answer is QR is, 44 inches.