Question

If sinx= 5/13 and x is in quadrant 1, then Tanx/2=

OA. -5
O B. - 1/5
OC. 5
O D. 1/5

Answer 1

Answer: D: 1/5

Explanation:

sinx = 5/13

this ratio is special; it is a 5-12-13 right triangle, (pythagorean triple).

there is also a formula to find tan(x/2); It is tan(x/2) = ±
`\sqrt{(1-cosx)/(1+cosx) }`

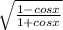
the + or - sign is decided by the quadrant the half angle is in;

since x is in quad one, it is somewhere between 0 and pi/2. To find the half angles position, simply divide it; x/2 is somewhere between 0/2 and pi/4.

so its also in the first quadrant. Since tangent is positive in the first quadrant, we will take the positive answer:

One more thing. we need the cosx in our formula. cosx will be 12/13, since this is a special right triangle as we said before.

tan(x/2) =
`\sqrt{(1-12/13)/(1+12/13) }`

tan(x/2) =
`\sqrt{(1/13)/(25/13) }`

tan(x/2)=
`√(1/25)`

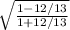
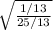
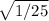
tan(x/2) = 1/5

Option D is the answer :)