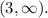Final Answer:
The curve
 is concave downward on the intervals
is concave downward on the intervals
 and
and
 .
.
Step-by-step explanation:
To determine the intervals where the given curve is concave downward, we need to analyze the second derivative. First, find the first derivative of the function
 :
:
![\[y' = x^2 - 9.\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/81qcrje10nmojeghd7dwyy2m2bi70cpw2g.png)
Now, find the second derivative:
![\[y'' = 2x.\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/87g5fp5su6ydrpmo3htvg0bflafvrp6deo.png)
For concavity, we are interested in the sign of the second derivative. The second derivative
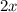 changes sign at
changes sign at
 . When
. When
 is negative, indicating concavity downward. Therefore, the curve is concave downward on the interval
is negative, indicating concavity downward. Therefore, the curve is concave downward on the interval
 . Similarly, when
. Similarly, when
 is positive, so the curve is concave downward on the interval
is positive, so the curve is concave downward on the interval
 .
.
However, we need to consider the points where the concavity changes. At
 and
and
 , the sign of the second derivative changes. Therefore, we exclude these points from the intervals. Combining these results, we get that the curve is concave downward on the intervals
, the sign of the second derivative changes. Therefore, we exclude these points from the intervals. Combining these results, we get that the curve is concave downward on the intervals
 and
and