Question

Thorium 234 is a radioactive isotope that decays according to the eqaution At=A0e^-10.498t, where A0 is the initial amount present and At is the amount present after t years. is the amount present after t years. If you begin with 1000 grams of strontium 90,

(a) How much thorium 234 will be left after 0.5 years? Round your answer to the nearest tenth of a gram.

------------------- grams


(b) When will 115 grams of thorium 234 be left? Round your answer to the nearest tenth of a year.

-------------------- years

Answer 1

(a) 5.3 grams

(b) 0.2 years

Explanation:

(a) Step 1: Since we're already given A0, we simply plug in 0.5 for t to find A(0.5), aka the amount of Thorium-234 remaining after 0.5 years:

`A(0.5)=1000e^(^-^1^0^.^4^9^8^*^0^.^5^)\\A(0.5)=1000e^(^-^5^.^2^4^9^)\\A(0.5)=5.252768542\\A(0.5)=5.3`

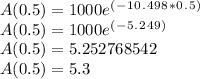
Thus, the amount of Thorium-234 remaining after 0.5 years is approximately 5.3 grams.

(b) We plug in 115 for A(t) and 1000 for A0. Then, we must solve for t: Thus, our equation to solve for t, time in years, is

`115=1000e^(^-^1^0^.^4^9^8^t^)`

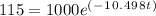
Step 1: Divide both sides by 1000.

115/1000 = e^(-10.498t)

0.115 = e^(-10.498t)

Step 2: Take the natural log (ln) of both sides.

ln(0.115) = ln(e^(-10.498t))

Step 3: According to the rules of natural logs, we can bring -10.498t down and multiply it by ln(e) on the right-hand side of the equation:

ln(0.115) = -10.498t * ln(e)

ln(0.115) = -10.498t * 1

ln(0.115) = -10.498t

Step 4: Now, we divide both sides by -10.498 and round the result to find out after about how many years will 115 grams of thorium-234 be remaining:

(ln(0.115) = -10.498t) / -10.498

0.2060223996 = t

0.2 = t

Thus, there will be 115 grams of thorium-234 remaining after about 0.2 years