Question

Rhombus ABCD has vertices A(-1, -2), B(2,2), C(6,5), and D(3,1). The perimeter of the rhombus is

Answer 1

The perimeter of the rhombus is approximately 19.999.

Explanation:

First of all, we plot all points that constructs the rhombus, whose outcome is attached below. Diagonals of the rhombus are segments AC and BD, whose lengths are determined by Pythagorean Theorem:

Segment AC

`AC = \sqrt{[6-(-1)]^(2)+[5-(-2)]^(2)}`

`AC \approx 9.899`

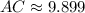
Segment BD

`BD = \sqrt{(3-2)^(2)+(1-2)^(2)}`

`BD \approx 1.414`

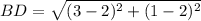
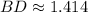
The perimeter of the rhombus (
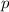`p`) is calculated by the following equation:

`p = 4\cdot \sqrt{\left((AC)/(2) \right)^(2)+\left((BD)/(2) \right)^(2)}`

`p = 2\cdot \sqrt{AC^(2)+BD^(2)}`

`p = 2\cdot \sqrt{9.899^(2)+1.414^(2)}`

`p \approx 19.999`

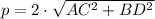
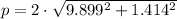
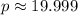
The perimeter of the rhombus is approximately 19.999.