Answer:
Magnitude: approximately
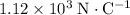 .
.
Direction: towards the negative point charge.
Step-by-step explanation:
By Coulomb's Law, at a distance of
 from a point charge of magnitude
from a point charge of magnitude
 , magnitude of the electric field would be:
, magnitude of the electric field would be:
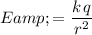 ,
,
Where
 is Coulomb's Constant.
is Coulomb's Constant.
In this question, it is given that:
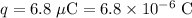 is the magnitude of the point charge, and
is the magnitude of the point charge, and
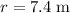 is the distance from the point charge.
is the distance from the point charge.
Substitute in the values (note the units) to find the magnitude of the electric field:
 .
.
At a given location, the direction of the electric field would be the same as the direction of the electrostatic force on a positive test charge at that very position.
For example, to find the direction of the electric field in this question, consider a positive test charge placed at the required location.
Charges of opposite signs attract each other. Hence, the hypothetical positive test charge would be attracted to the negative point charge with an electrostatic force pointing towards that negative charge. Direction of the electric field at that position would point in the same direction- towards the negative point charge.