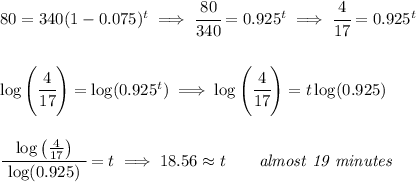Question

You bake bread until the internal temperature reaches 340F. The bread is placed on a table until the internal temperature reaches 80F and can be sliced. The room temperature is 68F and the cooling rate of the bread is r=0.075. How long do you have to wait until you can slice that bread?

Answer 1

ok, let's assume the rate is 0.075 per minute, if we convert that to percentage that'd be 0.075*100 or 7.5% per minute, so we can assume the bread is cooling off at 7.5% per minute after coming out of the oven at 340°F and we need it at 80°F so we can slice it and put some butter on it.

now, we can look at this from a Decay standpoint and say

we have a temperature of 340°F, decaying at 7.5% per minute, how long before it turns into 80°F?

`\qquad \textit{Amount for Exponential Decay} \\\\ A=P(1 - r)^t\qquad \begin{cases} A=\textit{current amount}\dotfill & \$ 80\\ P=\textit{initial amount}\dotfill &340\\ r=rate\to 7.5\%\to (7.5)/(100)\dotfill &0.075\\ t=minutes \end{cases}`

`80 = 340(1 - 0.075)^(t)\implies \cfrac{80}{340}= 0.925^t\implies \cfrac{4}{17}=0.925^t \\\\\\ \log\left( \cfrac{4}{17} \right)=\log(0.925^t)\implies \log\left( \cfrac{4}{17} \right)=t\log(0.925) \\\\\\ \cfrac{ ~~ \log\left( (4)/(17) \right) ~~ }{\log(0.925)}=t\implies 18.56\approx t\qquad \textit{almost 19 minutes}`