Question

NO LINKS!! URGENT HELP PLEASE!!!

8. Scott invested $1,600 into a retirement account that earns 2.4% interest compounded monthly. What will the balance of the account be after 30 years?

9. Kaylee used her graduation to set up a savings account that earns 3.4% interest compounded weekly. If the original amount deposited was $500, how much interest will she have earned after 10 years?

Answer 1

8) $3,284.73

9) $202.40

Explanation:

To solve both these problems, we can use the formula for compound interest:

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+(r)/(n)\right)^(nt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

Question 8

Given values:

• P = $1,600
• r = 2.4% = 0.024
• n = 12 (monthly)
• t = 30 years

Substitute the given values into the formula and solve for A:

`A=1600\left(1+(0.024)/(12)\right)^(12 \cdot 30)`

`A=1600\left(1+0.002\right)^(360)`

`A=1600\left(1.002\right)^(360)`

`A=3284.730430...`

`A=3284.73`

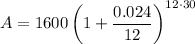
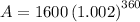
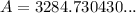
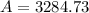
Therefore, the balance of Scott's account after 30 years will be $3,284.73.

`\hrulefill`

Question 9

Given values:

• P = $500
• r = 3.4% = 0.034
• n = 52 (weekly)
• t = 10 years

Substitute the given values into the formula and solve for A:

`A=500\left(1+(0.034)/(52)\right)^(52 \cdot 10)`

`A=500\left(1.000653846...\right)^(520)`

`A=702.3957509...`

`A=702.40`

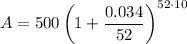
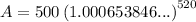
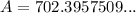
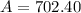
Therefore, the balance of the account after 10 years will be $702.40, which includes both the principal and the interest.

To find the amount of interest earned, subtract the principal:

Interest earned = $702.40 - $500 = $202.40

Therefore, Kaylee will have earned $202.40 in interest after 10 years.