Question

How to find critical points of f(x)= x^3 - 2x^2

Answer 1

x = 0 and x = 4/3

Step 1: First, we must find the derivative of f(x), noted by f'(x)

When you have a polynomial in the form x^n, we take the derivative of each polynomial using the following formula:

`f'(x)=nx^n^-^1`

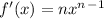
This means that the exponent becomes a coefficient and we subtract from the exponent.

We can do take the derivatives of x^3 and -2x^2 separately and combine them at the end:

x^3:

`x^3\\3x^3^-^1\\3x^2`

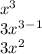
-2x^2

`-2x^2\\-2(2x^2^-^1)\\-4x`

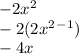
Thus, f'(x) is 3x^2 - 4x

Step 2: Critical points are found when f'(x) = 0 or when f'(x) = undefined. There are no values for x which would make 3x^2 - 4x undefined, so we can set the function equal to 0 and solving will give us our critical points

We see that we can factor out x from 3x^2 - 4x to get

x(3x - 4) = 0

Now, we can set the two expressions equal to 0 to solve for x:

Setting x equal to 0:

x = 0

Setting 3x - 4 equal to 0:

3x - 4 = 0

3x = 4

x = 4/3

Therefore, the two critical points of the function are x = 0 and x = 4/3