Complete Question
A child throws a ball with an initial speed of 8.00 at an angle of 40.0° above the horizontal. The ball leaves her hand 1.00 m above the ground and experience negligible air resistance. (a) What is the magnitude of the ball's velocity just before it hits the ground? (b) At what angle below the horizontal does the ball approach the ground?
Answer:
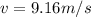
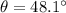
Step-by-step explanation:
From the question we are told that
Angle of ball
Height of ball h=1m
Generally the equation for vertical component is mathematically given by
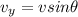
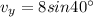
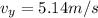
Generally the equation for horizontal component is mathematically given by

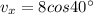

Generally the equation for vertical displacement of ball is mathematically given by
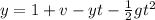
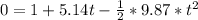
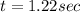
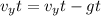
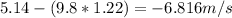
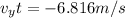
Generally the velocity of ball before it hits the ground is mathematically given by
Magnitude
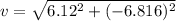
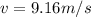
Direction of ball
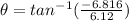
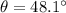 beneath the horizontal
beneath the horizontal