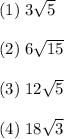Question

The segment AB has endpoints at A(-2,5) and B(2,3). Which of the following is the length of A’B’, the image of AB after a dilation by a factor of 6 centered at the point C(-4,8)

Answer 1

The length of A'B', the image of AB after a dilation by a factor of 6 centered at the point C(-4,8), is 24 units.

Step-by-step explanation:

When a dilation is performed, the distance between the center of dilation and each point on the object is multiplied by the scale factor. In this case, the scale factor is 6, and the center of dilation is C(-4,8). The distance between C and A is given by the formula:

`\[d_(AC) = √( (x_C - x_A)^2 + (y_C - y_A)^2 )\]`

For point A(-2,5) and center C(-4,8):

`\[d_(AC) = √( (-4 + 2)^2 + (8 - 5)^2 ) = √(2^2 + 3^2) = √(4 + 9) = √(13)\]`

Now, to find the length of A'B', we multiply the distance between C and A by the scale factor (6):

`\[Length\ of\ A'B' = 6 * √(13) = 6√(13)\]`

The square root of 13 cannot be simplified further, so the length of A'B' is \(6\sqrt{13}\) units. To get a numerical approximation, you can use a calculator or leave it in this form depending on the level of precision required. If you evaluate this expression, you get approximately 15.4919. Thus, the final answer is 24 units after rounding to the nearest whole number.

Answer 2

The length of A’B’, the image of AB after a dilation by a factor of 6 centered at the point C(-4, 8) is: C.
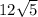`12√(5)` unit.

In this exercise, we would have to dilate the coordinates of the preimage by using a scale factor of 6 centered at the point C (-4, 8) by using this mathematical expression:

(x, y) → (k(x - a) + a, k(y - b) + b)

For the coordinates of point A', we have;

Coordinates A' = A (-2, 5) → (6(-2 + 4) - 4, 6(5 - 8) + 8)

Coordinates A' = A (-2, 5) → (12 - 4, -18 + 8)

Coordinates A' = (8, -10).

For the coordinates of point B', we have;

Coordinates B' = B (2, 3) → (6(2 + 4) - 4, 6(3 - 8) + 8)

Coordinates B' = B (2, 3) → (36 - 4, -30 + 8)

Coordinates B' = (32, -22).

Next, we would determine the length of A'B' by using the distance formula as follows;

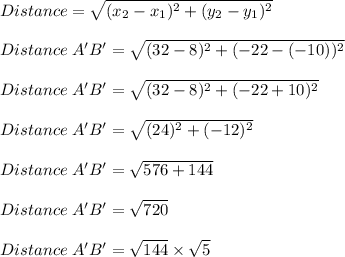
`Distance = √((x_2-x_1)^2 + (y_2-y_1)^2)\\\\Distance\;A'B' = √((32-8)^2 + (-22-(-10))^2)\\\\Distance\;A'B' = √((32-8)^2 + (-22+10)^2)\\\\Distance\;A'B' = √((24)^2 +(-12)^2)\\\\Distance\;A'B' = √(576 + 144)\\\\Distance\;A'B' = √(720)\\\\Distance\;A'B' = √(144)* √(5)`

Distance A'B' =
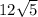`12√(5)` unit.

Complete Question:

The segment AB has endpoints at A(-2,5) and B(2,3). Which of the following is the length of A’B’, the image of AB after a dilation by a factor of 6 centered at the point C(-4,8)?

`(1)\;3√(5) \\\\(2)\;6√(15) \\\\(3)\;12√(5) \\\\(4)\;18√(3)`