Question

The area of the rectangle is 85 square centimeters. The length of the rectangle is (x - 12) cm and the width of the rectangle is x cm. Find the value of x.

Answer 1

x=17

Explanation:

To solve this we need to remember one thing. First, the area of a rectangle is lw=A. So to solve this we need to use this formula.

So, the length is (x-12) and the width is (x) we can multiply this by each other and set it equal to 85 to solve. We are trying to work backward from the solution to the problem. So let us do this

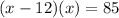`(x-12)(x)=85\\\\` - The next step is to distribute the x into the problem

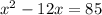`x^2-12x=85` - So now we have rewritten this problem, the next step is to subtract 85 from both sides. We are going to have a quadratic and will need to use the quadratic formula.

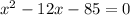`x^2-12x-85=0` - Now let us use the quadratic formula. The formula states:

`x=(-b+-√(b^2-4ac) )/(2a)`

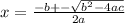
a is the confinement of
`x^2`. b is the number in front of the x. The c is the constant. In this problem is 1, b is -12 and c is -85.

Now that we know this we can insert this into the formula.

`x=(-b+-√(b^2-4ac) )/(2a)\\\\x=(-(-12)+-√((-12)^2-4(1)(-85)) )/(2(1))\\\\x=(12+-√(144+ 340) )/(2)\\\\x=(12+-√(484) )/(2)\\\\x=(12+-22)/(2)\\\\x=(12+22)/(2) , x=(12-22)/(2)\\\\x=(34)/(2) , x=(-10)/(2)\\\\x=17 , x=-5\\`

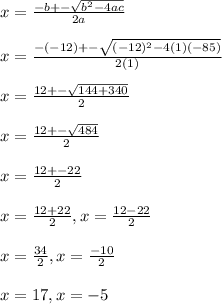
Because we are dealing with length, we know the value cannot be negative so our answer for x is 17.