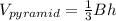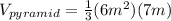Question

Find the volume of this triangle

Answer 1

14 cubic meters

Explanation:

Notation: Throughout this explanation, there are two very different "BASES". To try to keep ideas separate, I'm going to spell the 2-D shape Base with a capital B, and spell the 1-D length of the "base" of that 2-D triangle Base with a lower-case b.

This shape is a pyramid (a certain 2-D shape forms the Base, with layers that are similar shape all the way up, that comes up to a single point).

The formula for the Volume of a Pyramid is:

`V_(pyramid)=(1)/(3)Bh`

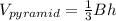
Where B is the area of the Base, and h is the height (the distance from the tip top, down to the base, where that line segment is "perpendicular" to the Base)

Finding the area of the "Base" shape (a 2-D triangle)

The shape of the Base is a right triangle.

The Area of a triangle is
`A_(triangle)=(1)/(2)bh`, where "b" is the "base" of the triangle, and "h" is the height of that triangle (the distance from the top of the triangle, down to the base, where that line segment is perpendicular to the base).

We can use the line segment that is length 4 as "b" the base of the triangle, and the line segment of length 3 as "h" the height of that triangle, to find the area of the Base of the Pyramid.

`A_(triangle)=(1)/(2)(4 m)(3 m)`

`A_(triangle)=6 m^2`

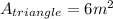
Finding the volume of the "Pyramid" (3-D)

For the volume of the Pyramid, the line segment that is length "7" is the distance from the tip top down to the Base and is perpendicular to the Base.

So,

`V_(pyramid)=(1)/(3)Bh`

`V_(pyramid)=(1)/(3)(6m^2)(7m)`

`V_(pyramid)=14m^3`