Answer:
15 points
Explanation:
The start and end point of the caterpillar path are;
Start point = (-3, -4)
End point = (25, 38)
The slope of the caterpillar's path, 'm', given the 'x', and y-coordinates of two points is given by the following formula;
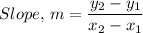
Therefore, m = (38 - (-4))/(25 - (-3)) = 1.5
The equation of the caterpillar's path in point and slope form is given as follows;
y - (-4) = 1.5 × (x - (-3))
y + 4 = 1.5 × (x + 3)
y + 4 = 1.5·x + 4.5
y = 1.5·x + 4.5 - 4 = 1.5·x + 0.5
y = 1.5·x + 0.5
Given that the 0.5 is added to the product of 'x' and 1.5, the points that have both integer points for 'x', and 'y' are the points that have odd number values of 'x', as follows;
(-3, -4), (-1, -1), (1, 2), (3, 5), (5, 8), (7, 11), (9, 14), (11, 17), (13, 20), (15, 23), (17, 26), (19, 29), (21, 32), (23, 35), (25, 38)
Therefore, we have 15 points counting the start and end points with integer coordinates