Question

Solve for x.


`\rm \longrightarrow \frac{x}{ \sqrt{ {x}^(2) + 1} } = {x}^(4) - x`
Best answer will be rewarded. ​

Answer 1

Factorize both sides of the equation:

`\frac x{√(x^2+1)} = x^4 - x`

`\frac x{√(x^2+1)} = x(x^3-1)`

`\frac x{√(x^2+1)} - x(x^3-1) = 0`

`x \left(\frac1{√(x^2+1)} - (x^3 - 1)\right) = 0`

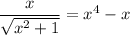
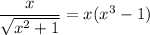
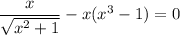
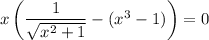
One immediate solution is then x = 0. This leaves us with

`\frac1{√(x^2+1)} - (x^3 - 1) = 0`

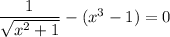
or as we had earlier,

`\frac1{√(x^2+1)} = x^3 - 1`

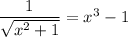
Take the square of both sides:

`\frac1{x^2+1} = \left(x^3-1\right)^2`

`\frac1{x^2+1} = x^6 - 2x^3 + 1`

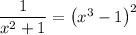
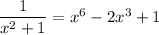
Turn this into a polynomial equation:

`1 = \left(x^2+1\right) \left(x^6-2x^3+1\right)`

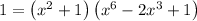
Expand the right side and make it equal to zero:

`1 = x^8 + x^6 - 2x^5 - 2x^3 + x^2 + 1`

`0 = x^8 + x^6 - 2x^5 - 2x^3 + x^2`

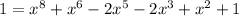
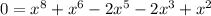
Each term in the polynomial has a common factor of x². Factoring this out just gives x = 0 again as a solution.

`0 = x^2 \left(x^6 + x^4 - 2x^3 - 2x + 1\right)`

`0 = x^6 + x^4 - 2x^3 - 2x + 1`

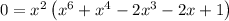
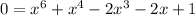
You'll need a computer to solve the remain se.xtic equation. Solving over reals, you would find two solutions, x ≈ 0.438 and x ≈ 1.18, but only x ≈ 1.18 is valid.

Answer 2

• x = 0 and x = 1.181

Explanation:

Another solution is graphical.

Take either side as a function and find the intersection of the graphs.

Use graphing software to make it much easier.

See below