Question

consider the functions given below. P(x)= 2/3x-1 Q(x)= 6/-3x+2 Match the expression with its simplified form​

Answer 1

P/Q = (-3x +2)/(3(3x -1))

PQ = 12/((3x -1)(-3x +2))

Explanation:

You want the quotient and product of P(x) = 2/(3x -1) and Q(x) = 6/(-3x +2).

Quotient

The quotient is found by multiplying by the inverse of the denominator:

`P(x)/ Q(x)=\left((2)/(3x-1)\right)/\left((6)/(-3x+2)\right)=\left((2)/(3x-1)\right)*\left((-3x+2)/(6)\right)\\\\\\(2(-3x+2))/(6(3x-1))=\boxed{(-3x+2)/(3(3x-1))}`

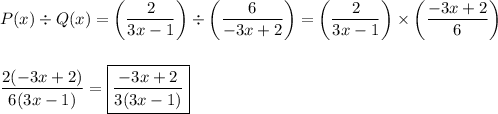
Product

As with multiplying any fractions, the numerator is the product of the numerators, and the denominator is the product of the denominators.

`P(x)* Q(x)=\left((2)/(3x-1)\right)*\left((6)/(-3x+2)\right)=(2\cdot 6)/((3x-1)(-3+2))\\\\\\=\boxed{(12)/((3x-1)(-3x+2))}`

__

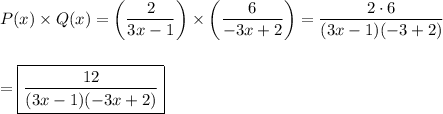
Additional comment

Usually the simplified form would contain no parentheses. The indicated products would be multiplied out.