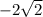Question

√18-√50 simplify the radical expression

Answer 1

`-2√(2)`

Explanation:

Main concepts

Concept 1. Radical Terminology

Concept 2. simplifying radicals

Concept 3. Combining like terms

Concept 1. Radical Terminology

For a radical like
`\sqrt[3]{5}`, the "3" (the number written in the little nook) is called the index of the radical, and the "5" (the number/expression) inside of the radical is called the radicand.

Concept 2. simplifying radicals

Note that for our given expression, the index is not explicitly written for either radical. By default, the index is 2. If we wrote them in explicitly, the expression would look like this:
`\sqrt[2]{18}-\sqrt[2]{50}`

To simplify radicals by hand, factor the radicand (usually completely down to primes), and form groups of matching numbers where the group size is the index of the radical. In this case, the index is "2", so we're looking for pairs of numbers that match after we factor (if it were a cube root, we'd be looking for triplets):

Factoring the first radicand

18

= 3*6

= 3 * 3*2

= (3*3) * 2

Factoring the second radicand

50

= 2 * 25

= 2 * 5*5

= 2 * (5*5)

So, we can rewrite our expression as follows:

`\sqrt[2]{(3*3)*2}-\sqrt[2]{2*(5*5)}`

Once you've found a group that matches (again, in this case, pairs), it can be factored out of the radical (only bring out one number/letter from each group to represent the group).

From the first radical, we have a pair of 3s, so it would simplify to
`3\sqrt[2]{2}`

Similarly, in the second radical, we have a pair of 5s, so it would simplify to
`5\sqrt[2]{2}`

So, altogether, our expression would simplify to the following at this point...

`3\sqrt[2]{2}-5\sqrt[2]{2}`

Side note: If everything factored out of the radical, it was a perfect "index" number (in this case, a perfect square number). If this happens, there is no radical left over at the end, and all of the numbers that were factored out, multiply together to make the answer.

Since we're done factoring numbers out of each radical, we don't need the index for each radical written in explicitly to remind us what size group we need, so let's remove them again, and let it be blank to represent the default index of "2".

`3√(2)-5√(2)`

Concept 3. Combining like terms

Notice that both 3, and the negative 5 are multiplied to a short expression, and that that expression,
`√(2)`, is exactly the same in both cases. This means we could apply the "reverse" distributive property and factor
`√(2)` out of both terms...

`(3-5)√(2)`

For some people, it can be easier to think of subtraction as addition of a negative number, so we'll rewrite it:

`(3+(-5))√(2)`

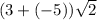
Adding positive and negative numbers together, the number with the larger magnitude (the -5 in this case), determines the sign of the result. The result is then just the difference of the two numbers' magnitudes, with the appropriate sign: -2

So the final simplified expression would be:
`-2√(2)`

Answer 2

the answer will be

Explanation:

`√(18) - √(50) \\ 3 √(2) - 5 √(2) \\ (3 - 5) √(2) \\ - 2 √(2) is \: the \: answer`