Answer:
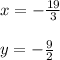
Explanation:
- Because the two equations are both in the slope-intercept form (y = mx + b, where m is the slope and b is the y-intercept), we can first find x by setting the two equations equal to each other:
g(x) = h(x)
-7/4x -187/12 = 9/5x + 69/10
Step 1: Add -187/12 to both sides of the equation
(-7/4x -187/12 = 9/5x + 69/10) + 187/12
-7/4x = 9/5x + 1349/60
Step 2: Subtract 9/5x from both sides of the equation
(-7/4x = 9/5x + 1349/60) - 9/5x
-71/20x = 1349/60
Step 3: Divide both sides of the equation by -71/20 to solve for x
(-71/20x = 1349/60) / -71/29
x = -19/3
- Now that we've found the x-coordinate of the intersection point, we can plug in -19/3 for x into any of the two equations to find the y-coordinate of the intersection point
- Let's try the g(x)
g(-19/3) = -7/4(-19/3) -187/12
g(-19/3) = 133/12 - 187/12
g(-9/2) = -9/2
Thus the point (x, y) at which they intersect is (-19/3, -9/2)
Optional Final Step
- We can check that the points we found are the intersection point by plugging in -19/3 for x in both equations and seeing whether the result we get is -9/2 for both equations
g(-19/3)
-9/2 =-7/4(-19/3) - 187/12
-9/2 = 133/12 - 187/12
-9/2 = -9/2
h(-19/3)
-9/2 = 9/5(-19/3) + 69/10
-9/2 = -57/5 + 69/10
-9/2 = -9/2