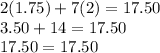Question

At a concession stand, seven hot dogs and two hamburgers cost $16.25; two hot dogs and seven hamburgers cost $17.50. Find the cost of one hot dog and the cost of one hamburger.

Answer 1

cost of one hamburger = $2.00; cost of one hot dog = $1.75

Explanation:

We can use a system of equations to find the cost of hot dog (represented by the variable, h) and the cost of one hamburger (represented by the variable, b)

We know that:

• the price of 7 hot dogs + the price of 2 hamburgers = total cost of $16.25,
• so the equation for this info is 7h + 2b = 16.25
• while the price 2 hot dogs + the price of 7 hamburgers = total cost of $17.50
• so the equation for this info is 2h + 7b = 17.50

Thus, our two equations are 7h + 2b = 16.25 and 2h + 7b = 17.50.

Method:

• We can use elimination to solve first for b (cost of one hot dog) by
• multiplying the entire first equation by 2
• and multiplying the entire second equation by -7
• This will cancel out the hs, since the least common factor of 7 and 2 is 14 and 14 + (-14) = 0:

`2(7h+2b=16.25)\\-7(2h+7b=17.50)\\\\14h+4b=32.50\\-14h-49b=-122.50\\\\-45b=-90\\b=2`

• Now that we've found the cost of one hamburger (2), we can plug in 2 for b in any of the two equations to find the cost of one hot dog
• We can try the first equation:

`7h+2(2)=16.25\\7h+4=16.25\\7h=12.25\\h=1.75`

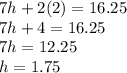
Optional Step: We can check that our answers are correct by plugging in 2 for b and 1.75 for h in both equations and see whether we get 16.25 for the first equation and 17.50 for the second equation.

Checking solutions for first equation:

`7(1.75)+2(2)=16.25\\12.25+4=16.25\\16.25=16.25`

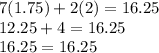
Checking solutions for second equation:

`2(1.75)+7(2)=17.50\\3.50+14=17.50\\17.50=17.50`