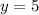Answer:
y=5
Explanation:
For two triangles to be congruent, the three angles of one triangle must be congruent to the three angles of the other triangle, AND the three side lengths of one triangle must be congruent to the three side lengths of the other triangle.
Notice that the three angles in each triangle have markings with little arcs. This is shorthand to represent that the angles are congruent to other angles with the same number of arcs. Therefore,
- angle E and angle H (each with one arc) are congruent,
- angle G and angle K (each with two arcs) are congruent,
- angle F and angle J (each with three arcs) are congruent.
So, this means that for the sides to match up, it will be easier to imagine rotating the second triangle counter clockwise so it is in the same orientation.
Side EG of Triangle 1 and Side HK of Triangle 2 are both 31 mm.
Side GF of Triangle 1 and Side KJ of Triangle 2 are both 24 mm.
So, in order for the two triangles to be congruent, side EF of Triangle 1 and Side HJ of Triangle 2 must be the same length.
Since we're asked to find the value of the variable that results in congruent triangles, we'll set the expressions equal to each other


Add 10 to both sides...
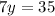
Divide both sides by 7...