Answer:
x=1
Explanation:
Main concept: Solving a one-variable equation with multiple instances of the unknown
For any equation in math where there is only one item that is unknown, (even if it shows up multiple times in the equation), there are two main steps:
Step 1. Get the variable to show up exactly once
Step 2. Isolate the variable
Step 1. Get the variable to show up exactly once
Since we know that in the very end, we want x=__, we know that the x will appear only once (and thus only on one side of the equation, not both), and will be by itself.
In practice, sometimes there are special tricks that have to be employed to make this step happen. Generally, this means simplify each side of the equation, and try to group like terms together.
For this equation, observe that x appears twice: once on the left side of the equation, and once on the right side of the equation.
At some point, we'll need to get the "x"s on the same side of the equation, and hopefully combine like terms into a single term with x.

First, let's explicitly write out the multiplication sign that is hiding between the 2 and the parenthesis:

A common mistake would be to try to subtract the 2 from 6 but remember that order of operations states that multiplication should happen before subtraction.
Let's rewrite the subtraction as addition of a negative number...

Apply the distributive property...

-2*2 is -4, and -(-2)*x is positive 2x...

While it's true that Order or Operations states that parentheses would be done before the addition of the 6, there is an associative property of addition which allows us to regroup the three terms (since all 3 terms are added, we can add in any order).

6+(-4) is 2...

At this point, we've simplified the right side as much as we can, and it will be easy to move the term with the "x" in it to the other side of the equation.
Currently, the term with the "x" on the right side is added to the other term, so we'll subtract an equivalent amount of "x"s from both sides of the equation...

While we technically can't immediately apply the associative property of addition here (since it isn't all addition) we can re-imagine the subtraction, as adding a negative number...

Now the associative property of addition can be applied...

On the right side of the equation, combining like terms will zero out, leaving just the 2. On the left side of the equation, combining like terms will leave 2x...

At this point, we've completed Step 1 of solving a one-variable equation (getting the variable to show up exactly once -- this is often the part that takes more work).
Step 2. Isolate the variable
From here, we just need to isolate the variable. Notice that the 2 is attached to the "x". It is attached by multiplication (albeit not explicitly written, it is implied multiplication).

To undo the multiplication, apply the opposite operation (division) by dividing both sides of the equation by 2.

If you focus on the left hand side only and imagine x as a number, x is multiplied by 2, and then immediately divided by 2, which would bring you right back to the original value you started with (x). So the left side simplifies to "x", an the right side simplifies to 1 (because any non-zero number divided by itself is 1). So, the equation simplifies to...
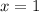
Verifying the answer:
To verify an answer, plug it back into the original equation for each instance of the variable. Evaluate each side of the equation separately, and make sure that the left side does equal the right side. If so, we're right. If not, it's not a solution (and/or something went wrong).
Left side:



Right side:





So, both sides are equal, and the equation is true. Thus, x=1 is a solution.