Factorize both sides of the equation:
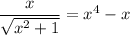
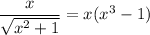
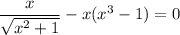
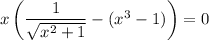
One immediate solution is then x = 0. This leaves us with
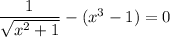
or as we had earlier,
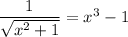
Take the square of both sides:
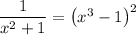
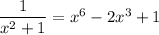
Turn this into a polynomial equation:
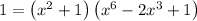
Expand the right side and make it equal to zero:
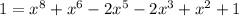
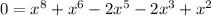
Each term in the polynomial has a common factor of x². Factoring this out just gives x = 0 again as a solution.
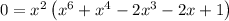
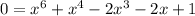
You'll need a computer to solve the remain se.xtic equation. Solving over reals, you would find two solutions, x ≈ 0.438 and x ≈ 1.18, but only x ≈ 1.18 is valid.