Question

A radioactive substance has an initial mass of 110 grams and a half-life of 6 days.

What equation is used to determine the number of days, x, required for the substance to decay to 53 grams?

Enter your answer by filling in the boxes.

Answer 1

`53 = 110 \left((1)/(2)\right)^{(x)/(6)}`

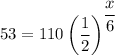
Explanation:

The decay of a radioactive substance can be modeled using the half-life formula:

`\large{\boxed{N(t)=N_0\left((1)/(2)\right)^{(t)/(t_(1)/(2))}}}`

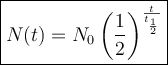
where:

• N(t) is the quantity of the substance remaining after time t.
• N₀ is the initial quantity of the substance.
• t is the time elapsed.
• t_{1/2} is the half-life of the substance.

In this case, the initial amount of substance is N₀ = 110 grams and the half-life is t_{1/2} = 6 days.

To find the number of days, x, required for the substance to decay to 53 grams, we can set N(t) = 53 and t = x.

Therefore, the equation that can be used to determine the number of days, x, required for the substance to decay to 53 grams is:

`\boxed{53 = 110 \left((1)/(2)\right)^{(x)/(6)}}`

`\hrulefill`

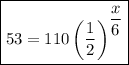
To solve the equation, divide both sides by 110:

`\left((1)/(2)\right)^{(x)/(6)}=(53)/(110)`

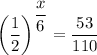
Take natural logarithms of both sides:

`\ln \left((1)/(2)\right)^{(x)/(6)}=\ln (53)/(110)`

`\textsf{Apply the power law:} \quad \ln x^n=n \ln x`

`(x)/(6)\ln \left((1)/(2)\right)=\ln \left(\frac {53}{110}\right)`

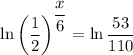
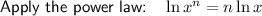
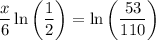
Multiply both sides by 6:

`x\ln \left((1)/(2)\right)=6\ln \left((53)/(110)\right)`

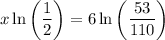
Divide both sides by ln(1/2):

`x=(6\ln \left((53)/(110)\right))/(\ln \left((1)/(2)\right))`

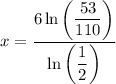
Evaluate:

`x=6.32063555...`

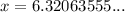
Therefore, the number of days required for the substance to decay to 53 grams is approximately 6.32 days, as calculated using the half-life formula.