Answer:
D. x ≈ 2.75
Explanation:
You want to approximate the solution to 2√(x-1) +2 = 3x/(x -1) to the nearest 1/4 unit using a table of values.
Zero
We find it often simplifies the process of finding solutions if we rewrite the equation so we are looking for the difference between the left side and right side to be zero:
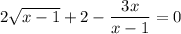
It is convenient to define a function f(x) equal to the left-side expression here. This means we're looking for x that satisfies f(x) = 0.
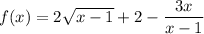
Guess
The smallest integer in the domain is x = 2, so we can start with that value to see what the function looks like:
f(2) = 2√(2 -1) +2 -3(2)/(2 -1) = 2 +2 -6 = -2
For larger x, the radical expression will get larger and the rational expression will get smaller:
f(3) = 2√(3 -1) +2 -3(3)/(3 -1) = 2√2 +2 -9/2 = √8 -5/2 ≈ 0.33
This tells us the solution lies between 2 and 3, and is probably closer to 3. Using the method of bisecting the interval containing the solution, we find ...
f(2.5) ≈ -0.55
f(2.75) ≈ -0.07
This value is closer to zero than f(3), so we choose x ≈ 2.75 as the value of x closest to the solution to the equation.
__
Additional comment
It is convenient to have a calculator or spreadsheet do the repeated evaluation of the function f(x). The table of the above iterated values is shown in the first attachment.
Perhaps strictly speaking, "using a table of values" means you want to evaluate the equation for some set of x-values without regard to where the root might be. Then you choose the result that best matches the one desired. The second attachment shows that approach, with a spreadsheet doing the arithmetic.
Further iteration gives a root of x ≈ 2.79009504299.