Final Answer:
The function
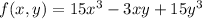 has no points where both
has no points where both
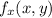 and
and
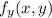 are equal to zero simultaneously.
are equal to zero simultaneously.
Explanation:
To find the critical points where both partial derivatives are zero, we compute
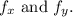
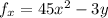
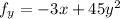
Setting both equations to zero to find critical points:
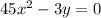
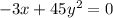
From the first equation,
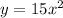 . Substituting this into the second equation gives
. Substituting this into the second equation gives
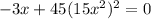
Simplifying, we get
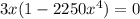
This implies
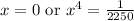
The value
 yields
yields
 from
from
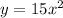 , giving a point (0, 0).
, giving a point (0, 0).
For
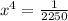 , there are no real solutions within the domain.
, there are no real solutions within the domain.
Hence, the function
 has only one critical point at (0, 0), where neither
has only one critical point at (0, 0), where neither
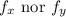 are zero. This implies that there are no points where both partial derivatives are zero simultaneously.
are zero. This implies that there are no points where both partial derivatives are zero simultaneously.