Question

A potter's wheel is spinning with an initial angular velocity of 14 rad/srad/s . it rotates through an angle of 80.0 radrad in the process of coming to rest.What was the angular acceleration of the wheel?

How long does it take for it to come to rest?

Answer 1

Angular acceleration: approximately
`1.225\; {\rm s^(-2)}`.

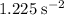The wheel stopped after approximately
`11.4\; {\rm s}`.

(Assuming that the angular acceleration of the wheel is constant.)

Step-by-step explanation:

Rearrange the following equation to find the angular acceleration of this wheel:

`2\, a\, x = v^(2) - u^(2)`,

Where:

• 
  `a` is the angular acceleration (to be found,)
• 
  `x` is the rotational displacement,
• 
  `v` is the final rotational velocity, and
• 
  `u` is the initial rotational velocity.

In this question, it is given that
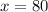`x = 80` and
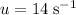`u = 14\; {\rm s^(-1)}`. Additionally,
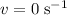`v = 0\; {\rm s^(-1)}` since the wheel has stopped rotating. Rearrange the equation to find
`a`:

`\begin{aligned}a &= (v^(2) - u^(2))/(2\, x) \\ &= ((0)^(2) - (14)^(2))/(2\, (80))\; {\rm s^(-2)} \\ &= 1.225\; {\rm s^(-2)}\end{aligned}`.

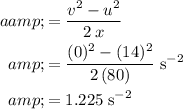Divide the change in angular velocity
`(v - u)` by angular acceleration to find the time required:

`\begin{aligned} t &= (v- u)/(a) \\ &= (0 - 14)/((-1.225))\; {\rm s} \\ &\approx 11.4\; {\rm s}\end{aligned}`.