Question

Find the taylor polynomial t3(x) for the function f centered at the number a. f(x) = xe−7x, a = 0

Answer 1

To calculate the Taylor polynomial of degree 3 for the function
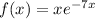`f(x) = xe^(-7x)` centered at a=0, evaluate the function and its first three derivatives at x=0. Substitute these values into the Taylor series formula to get t3(x) = x - ¼ x² + ⅛ x³.

Step-by-step explanation:

To find the Taylor polynomial t3(x) for the function f(x) = xe−7x centered at a=0, we need to compute the function and its derivatives at x=0, up to the third derivative, and then use the Taylor series formula.

First, f(x) = xe−7x, so f(0) = 0.

The first derivative is f'(x) = e−7x − 7xe−7x, and f'(0) = 1.

The second derivative is f''(x) = −14e−7x + 49xe−7x, and f''(0) = −14.

The third derivative is f'''(x) = 98e−7x − 343xe−7x, so f'''(0) = 98.

Using these values, the Taylor polynomial of degree 3 is:

t3(x) = f(0) + f'(0)x + ½ f''(0)x² + ⅛ f'''(0)x³

t3(x) = 0 + 1⋅x − 7⋅½ x² + 98⋅⅛ x³

t3(x) = x − ¼ x² + ⅛ x³

Answer 2

To find the Taylor polynomial t3(x) for the function f(x) = xe^-7x centered at a = 0, we need to find the values of the function and its derivatives at x = a and substitute them into the Taylor polynomial formula. The Taylor polynomial t3(x) is x - 7(x^2) + 1715(x^3)/6.

Step-by-step explanation:

To find the Taylor polynomial t3(x) for the function f(x) = xe-7x centered at a = 0, we need to find the values of the function and its derivatives at x = a and substitute them into the Taylor polynomial formula. The Taylor polynomial t3(x) is a third-degree polynomial, so we need the first three derivatives of the function.

The derivatives of f(x) = xe-7x are f'(x) = e-7x - 7xe-7x, f''(x) = 49xe-7x - 14e-7x, and f'''(x) = 343e-7x - 98xe-7x.

Substituting x = 0 into the function and its derivatives, we get f(0) = 0, f'(0) = 1, f''(0) = -14, and f'''(0) = 343.

Finally, substituting these values into the Taylor polynomial formula, we have: t3(x) = f(0) + f'(0)(x - a) + rac{f''(0)(x - a)^2}{2!} + rac{f'''(0)(x - a)^3}{3!}
= 0 + 1(x - 0) + rac{-14(x - 0)^2}{2!} + rac{343(x - 0)^3}{3!}
= x - 7(x^2) + rac{1715(x^3)}{6}