Question

When comparing the f(x) = –x2 + 2x and g(x) = log(2x + 1), on which interval are both functions positive

(–∞, 0)
(0, 2)
(2, ∞)
(–∞, ∞)

Answer 1

B) (0, 2)

Explanation:

Given functions:

`f(x) = -x^2 + 2x`

`g(x) = \log(2x + 1)`

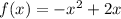
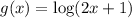
To find the interval on which both functions are positive, we need to consider where each function is greater than zero.

Function f(x)

Function f(x) is a quadratic function with a negative leading coefficient. This means it is a parabola the opens downwards. Therefore, f(x) is positive for all x-values within the interval defined by its x-intercepts.

Find the x-intercepts of the function by setting f(x) to zero and solving for x:

`\begin{aligned}f(x)& = 0\\-x^2+2x& = 0\\2x-x^2& = 0\\x(2-x)& = 0\\\\x&=0\\2-x&=0 \implies x=2\end{aligned}`

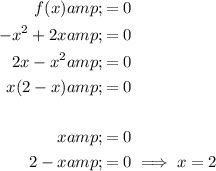
Therefore, function f(x) crosses the x-axis at x = 0 and x = 2, which means that the function is positive on the interval (0, 2).

Function g(x)

The logarithmic function is equal to zero when its argument is equal to one. Therefore, for function g(x) to be positive, its argument must be greater than 1:

`\begin{aligned}2x+1& > 1\\2x+1-1& > 1-1\\2x& > 0\\x& > 0\end{aligned}`

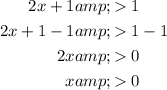
Therefore, function g(x) is positive when x > 0, so on the interval (0, ∞).

Interval

To determine the interval in which both f(x) and g(x) are positive, we must identify the overlapping portion of their respective intervals.

Therefore, the interval on which both functions are positive is (0, 2).