Question

Find the unit vector in the direction of v. v = -6.9i 3.3j

Answer 1

`< -0.902, 0.431 >`

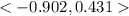
Explanation:

The unit vector of any vector is the vector that has the same direction as the given vector, but simply with a magnitude of 1. Therefore, if we can find the magnitude of the vector at hand, and then multiply
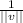`(1)/(||v||)`, where ||v|| is the magnitude of the vector, then we can find the unit vector.

Remember the magnitude of the vector is nothing but the pythagorean theorem essentially, so it would be
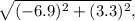`\sqrt{(-6.9)^(2) +(3.3)^(2) } ,` which will be
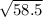`√(58.5)`. Now let us multiply the vector by 1 over this value, and rationalize to make your math teacher happy.
`< -6.9, 3.3 > * (1)/(√(58.5)) = < (-6.9√(58.5) )/(58.5) , (3.3√(58.5))/(58.5) >`

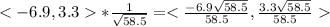
You can put those values into your calculator to approximate and get

`< -0.902, 0.431 >`

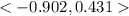
You can always check the answer by finding the magnitude of this vector, and see that it is equal to 1.

Hope this helps